En 2002, le prix Nobel d’économie fut attribué à Daniel Kahneman et à Vernon Smith pour leurs travaux en psychologie économique et en économie expérimentale. Depuis lors, cette branche de la science économique s’est fortement développée. L’une de ses originalités est l’importance qu’elle accorde à la méthode expérimentale. On peut ainsi mieux mesurer à quel point le comportement économique, individuel ou collectif, est dépendant des illusions, des préjugés, des passions des hommes. Peu à peu, nous voyons émerger une nouvelle description des conduites humaines, très éloignée du modèle classique de l’homo economicus, calculateur et rationnel.
Parmi les pulsions qui influencent le comportement économique, deux méritent particulièrement l’intérêt. Dans un premier article, je décrirai la découverte et les progrès de la connaissance d’un biais cognitif très répandu, l’aversion aux pertes. Un second biais cognitif, l’aversion à l’inéquité, sera prochainement traité.
Il est absolument nécessaire de les prendre en compte pour comprendre le fonctionnement réel de l’économie, analyser les décisions des acteurs, décrypter les débats et les choix politiques.
L’aversion aux pertes (loss aversion).
Après avoir reçu le prix Nobel d’économie, le psychologue Daniel Kahneman a popularisé ses travaux dans des livres pour le grand public. L’un d’entre eux, Thinking, Fast and Slow (2011 ; traduction française : Système 1 / Système 2. Les deux vitesses de la pensée), vendu à plus d’un million d’exemplaires, a connu un grand succès. Kahneman y oppose deux modes de réflexion, l’un rapide et gouverné par l’émotion -le Système 1-, l’autre plus lent et rationnel -le Système 2.
L’aversion aux pertes fait partie des biais cognitifs qui influencent notre Système 1, pour reprendre les mots de Kahneman. L’étude de ce biais cognitif a progressé grâce à lui et à son partenaire, l’économiste Amos Tversky, mais ils n’en sont pas les premiers découvreurs.
Le mot « biais » a ici le sens de « déformation » de la perception par le cerveau. Cette « déformation » inciterait le sujet à se comporter de façon « irrationnelle », c’est-à-dire de façon autre que ce que dicterait un raisonnement logico-mathématique. Je mets ces mots entre guillemets pour souligner qu’ils n’ont de pertinence que par rapport à une norme de comportement rationnel.
+Un peu d’histoire+
*1944 : Morgenstern et Von Neumann, Theory of Games and Economic Behaviour (Théorie des jeux et du comportement économique).
Dans ce livre fondateur de la théorie des jeux, les auteurs introduisent la notion de l’utilité espérée. Cette utilité espérée se définit comme l’espérance mathématique des gains et des pertes, c’est-à-dire, dans le cas de deux résultats possibles A et B, la moyenne de ces résultats pondérée par leur probabilité : (résultat A x probabilité de ce résultat) + (résultat B x probabilité de ce résultat), la somme des probabilités étant égale à 1.
Une distribution de probabilité (ensemble de résultats éventuels affectés chacun d’une probabilité) est préférable à une autre si son utilité espérée (espérance mathématique des résultats) est plus grande. La maximisation de cette utilité espérée est le critère auquel sont supposés se conformer les joueurs. Hypothèse sous-jacente : on présume que toutes les éventualités ont le même poids aux yeux de chaque joueur.
*1952-1953 : Maurice Allais met en évidence, sur la base d’une enquête auprès d’une centaine de personnes a priori jugées rationnelles, le « paradoxe d’Allais » ou « effet Allais » (communication en 1953 à une conférence de l’American Economic Society).
Au voisinage de la certitude, constate-t-il, on accorde plus d’importance à l’absence de perte que ce à quoi il faudrait s’attendre sur la base de l’utilité espérée : gagner 100 avec une probabilité de 100 % (utilité espérée 100) est préféré à gagner 150 avec une probabilité de 90 % et 0 avec une probabilité de 10 % (utilité espérée 135). Il en résulte que l’un des axiomes, dit d’indépendance, de la théorie de l’utilité espérée est en pratique souvent violé.
Définition : l’axiome d’indépendance énonce que l’ordre de préférence entre deux distributions de probabilité n’est pas modifié si on « mélange » chacune d’elles avec une même autre distribution de probabilité.
*1979 : Daniel Kahneman et Amos Tversky généralisent le paradoxe d’Allais, introduisent la notion d’aversion aux pertes (loss aversion) et présentent la première formulation de leur théorie dite des perspectives (Prospect theory).
La cohérence théorique de cette première version, toutefois, est rapidement mise en question.
*Années 1980 : de façon indépendante, Maurice Allais, complétant ses premières analyses, et deux autres chercheurs, Quiggin et Yaari, résolvent les questions théoriques laissées en suspens par la première présentation du paradoxe d’Allais.
*1992 : Kahneman et Tversky proposent une formulation révisée de la théorie des perspectives, reprenant les perfectionnements apportés par Allais et les deux autres chercheurs. C’est cette seconde version qui vaut à Kahneman le prix Nobel d’économie. Celui-ci aurait légitimement pu être partagé avec Maurice Allais, si ce dernier ne l’avait déjà obtenu pour d’autres travaux[[Voir à ce propos le récent article de Bertrand Munier, « Penser le risque aujourd’hui : l’apport novateur de Maurice Allais » (Commentaire, n° 176, Hiver 2021-2022), ici p. 800-801, et celui d’Éric Barthalon, « Le paradoxe d’Allais : une notoriété aussi universelle que justifiée » (Bulletin de la Sabix, 2e semestre 2020, en ligne, ici § 48). Tous deux sont assez réservés sur l’apport de Kahneman et Tversky à l’étude de ces questions.]].
Au vu de ces recherches, il apparaît clairement que la formule de calcul de l’utilité espérée doit être modifiée. Une double pondération doit y être intégrée : pondération donnant une valeur subjective à chaque gain ou perte ; pondération donnant une valeur subjective à chaque probabilité. Cela remet en cause la définition de la rationalité formulée par Morgenstern et Von Neumann : toutes les éventualités n’ont pas le même poids.
Ces déformations subjectives conduisent les sujets à réagir de façon dissymétrique aux perspectives de gain et de perte : ils ont une forte aversion aux pertes (acceptant, pour ne pas les comptabiliser, de prendre plus de risques) et une appétence modérée pour les gains (répugnant, pour les accroître, à prendre plus de risques de perte : « un bon tiens vaut mieux que deux tu l’auras »).
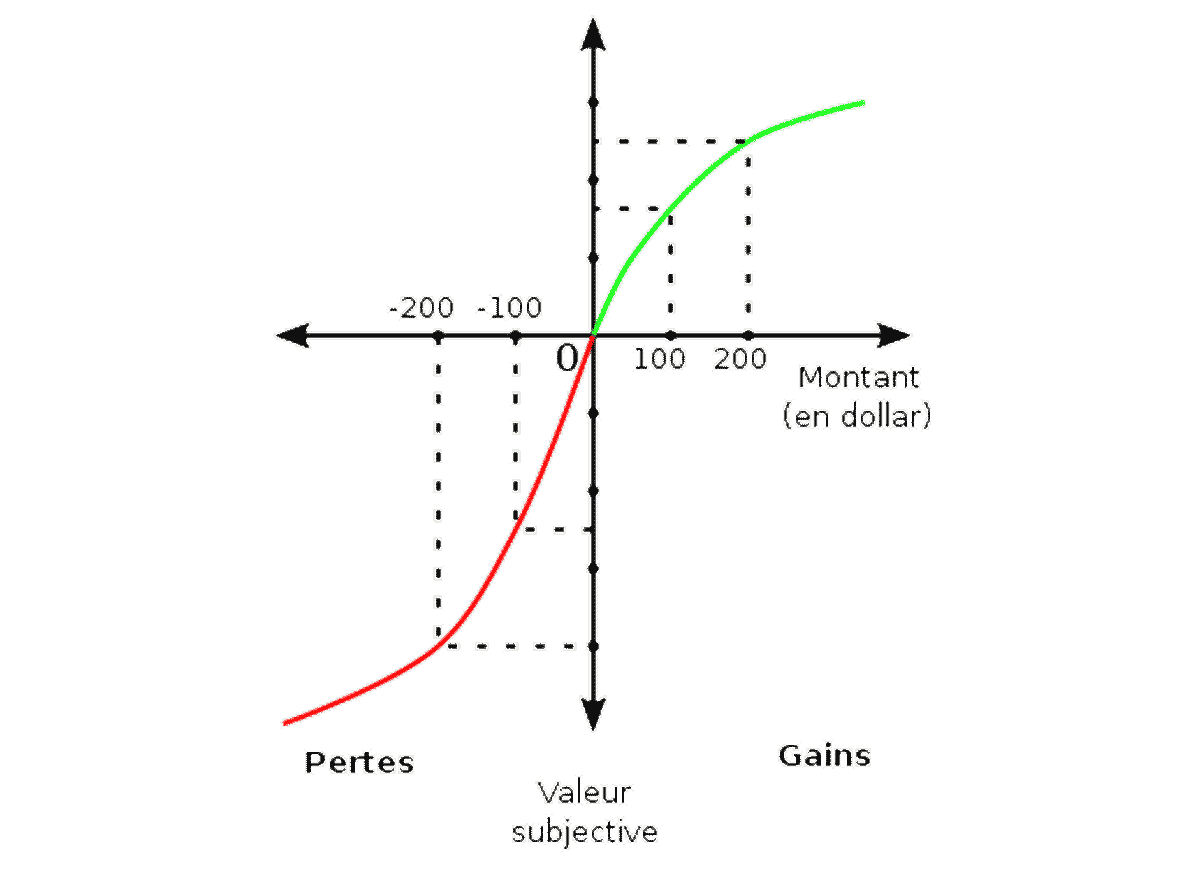
Dans les deux cas, le comportement subjectif (limiter les pertes, limiter les risques en situation de gain) témoignerait de ce qu’on pourrait appeler une « préférence pour la stabilité ».
On notera, au passage, que ces travaux remettent en cause l’idée que les lois de l’économie seraient les mêmes partout : les comportements diffèrent fortement aux deux bouts de l’échelle, au voisinage des très fortes et des très faibles probabilités.
+Expérimentations …+
Depuis les années 1970, de nombreux travaux de psychologie humaine expérimentale ont été menés sur ce thème. Les résultats ne semblent pas tous également convaincants. Le phénomène d’aversion aux pertes serait plus aisément vérifiable pour les pertes importantes que pour les plus faibles. Des explications alternatives ont été présentées, notamment avec le concept d’« attention aux pertes » : selon cette hypothèse, les risques de perte n’ont pas un poids subjectif plus important que les gains dans la prise de décision, mais ils éveillent plus d’attention dans la gestion d’une tâche ou d’une situation.
Des études plus récentes ont été menées sur les Primates. Keith Chen (2006)[[Keith Chen et al., « How Basic Are Behavioral Issues ? Evidence from Capuchin Monkey Trading Behavior », Journal of Political Economy, 2006, vol. 114, n° 3, p. 517-537. Les Capucins ou Sapajous, singes d’Amérique, ont été utilisés, à cause de leur grande intelligence et habileté, comme auxiliaires de vie de personnes tétraplégiques.]], après avoir acclimaté des singes capucins au maniement de la monnaie fiduciaire et à la pratique du commerce (en reproduisant des expériences antérieures montrant chez les singes des comportements économiques semblables à ceux des humains), a testé leur sensibilité aux pertes et aux gains. Il identifie chez eux un biais d’aversion aux pertes, dont la mesure (coefficient d’aversion) serait du même ordre de grandeur que celle habituellement trouvée chez l’espèce humaine. Amélie Romain (2015)[[Prise de décision en situation risquée ou ambigüe chez les primates. Thèse soutenue en janvier 2015, Université de Strasbourg (en ligne), p. 187-190.]] trouve des résultats analogues chez la majorité des espèces étudiées, avec, chez les Chimpanzés et les Bonobos, un coefficient d’aversion proche de celui des humains adultes (environ 1,5).
Définition : le coefficient d’aversion à la perte, généralement noté λ, mesure le rapport entre le ressenti de la perte et le ressenti du gain en situation risquée : égal à 1 en cas de neutralité entre le ressenti de la perte et du gain, il est supérieur à 1 en cas d’aversion aux pertes (jusqu’à 2 ou plus dans certaines études), inférieur à 1 dans le cas inverse.
+… et questionnements.+
Étant à la fois répugnant aux pertes et (en situation de gain) répugnant au risque, Homo sapiens serait-il spontanément conservateur ? et pour quelle(s) raison(s) ?
Si ces biais cognitifs s’observent aussi chez les Primates, ne faut-il pas en conclure qu’ils remontent à quelques millions d’années avant notre ère, époque de la séparation entre ces proches cousins et les ancêtres directs de notre espèce ? Dans ce cas, ces prétendus biais n’ont-ils pas eu en fait une grande rationalité, en favorisant des comportements propres à la survie, avec pour conséquence que nous sommes, aujourd’hui, encore là pour en discuter ? Quelle serait donc la logique profonde de tout cela, et quels mécanismes seraient ici à l’œuvre ?
La théorie de l’évolution, la neurologie, la théorie des jeux, la sociobiologie devraient nous fournir des outils pour répondre à ces questions. Quels que soient les développements futurs, l’aversion aux pertes est d’ores et déjà devenue un élément d’explication indispensable de certains comportements apparemment irrationnels des investisseurs : la difficulté de « prendre sa perte » sur un marché baissier en est un exemple. On peut aussi interpréter, avec ces mêmes outils d’analyse, des phénomènes très répandus comme les réflexes de défense des privilèges catégoriels ou des acquis sociaux. Lorsque le secrétaire général de la CGT, M. Philippe Martinez, s’oppose à toute réforme des régimes spéciaux de retraite, n’est-ce pas à la part de Chimpanzé ou de Bonobo qui est en nous qu’il s’adresse ?


2 commentaires
l’aversion aux pertes,
Bien documenté et très intéressant. Appliqué à la gestion du Covid , le coefficient lamda
tendrait vers deux surtout au gouvernement avec un risque de perte de vie surdimensionnés par rapport au plaisir de la liberté . N’est ce pas le sort de toute action dans un pays qui met le principe de précaution dans sa constitution ?
Intéressants rappels et synthèses
Merci pour cette belle généalogie des concepts popularisés par Kahneman.
Un élément important du livre de Kahneman, concerne la création d’une expertise pour le cerveau 1 dans un domaine délimité et le rendre plus fort et rapide que le cerveau 2 dans ce domaine. (et donc s’affranchir des biais, par ex oser mettre sa dame en prise).
Avec le piège, dans les autres domaines, que la même sensation d’avoir raison n’est pas liée avec avoir raison ou pas. Par ex, un spécialiste de la finance devenu Jupiter et ayant à couvrir tous les domaines…
Autre ouverture intéressante l’impact catastrophique sur le comportement des foules et des élus dans une démocratie. Là, l’expertise de la foule ne semble pas facile à construire ni à actualiser quand les contextes changent. Par ex l’expertise des 30 glorieuses en état fermé quand l’état est devenu ouvert et la mondialisation forte.
Les commentaires sont fermés.